论文笔记[3]——Computing a small agreeable set of indivisible items

文章：Pasin Manurangsi, Warut Suksompong, Computing a small agreeable set of indivisible items, Artificial Intelligence, Volume 268, 2019, Pages 96-114.

Agreeable set – necessarily agreeable set – agreeable set 一个最坏上界（证明 and 2和3情况的构造） – 计算necessarily agreeable set – 一般情形下求最小的agreeable set – 可加效用函数下的探讨.

准备工作

记号说明

$[n]$：代理人，编号为 $1,2,\cdots,n$；
$S=\{x_1,\cdots,x_m\}$：物品集合，$\mathcal{S}$ 表示其幂集；
偏好：每个代理人 $i$ 都被赋予了一个偏好关系 $\succeq_i$，用以比较 $S$ 子集之间的好坏关系. 偏好关系是自反、完全、和传递的；
$\begin{bmatrix}V \\ t\end{bmatrix}$ 表示集合 $V$ 的 $t$ 元子集族；

Necessarily agreeable set

对于necessarily agreeable set，有一个重要的命题：

Prop. 1. 取定 $\mathcal{S}$ 上的单物品偏好 $\succeq^{sing}$，不妨设为 \[x_1\succeq^{sing} x_2\succeq^{sing}\cdots\succeq^{sing} x_m.\] 令 $T\subset S$，记 $I_k=\{x_1,x_2,\cdots,x_m\}$，$\forall k=1,\cdots,m$，则有：
若 $\vert I_k\cap T \vert\geqslant k/2$，$\forall k=1,\cdots,m$，则 $T$ 在 $\succeq^{sing}$ 下是necessarily agreeable的.
当偏好 $\succeq^{sing}$ 是严格的，其逆命题也成立.

Proof. 先证 $\Rightarrow$：由条件可知 $|I_m\cap T|\geqslant m/2$，于是 $|T|\geqslant |S\backslash T|$. 取 $T'\in\begin{bmatrix}T \\ |S\backslash T|\end{bmatrix}$ 且 $T'$ 是其中下标最小的.
由此即可在 $T'$ 与 $S\backslash T$ 间定义一个保序的双射 $f:T'\to S\backslash T$，即下标最小的映射到下标最小的. 由于 $|I_k\cap T|\geqslant k/2$，$\forall k=1,\cdots,m$，故 $f$ 必定将 $x_k$ 映射到某个 $l>k$ 的 $x_l$. 由responsive的定义可知，任意一个与 $\succeq^{sing}$ 相容的responsive的偏好，都保持 $T'\succeq S\backslash T$. 又由于所有responsive的偏好都是单调的，故 $T\succeq S\backslash T$，即 $T$ 在 $\succeq^{sing}$ 之下是necessarily agreeable的.
再证 $\Leftarrow$：用反证法：假设存在 $l$，s.t. $|I_l\cap T|<1/2$. 取一个小常数 $\epsilon>0$，假设偏好 $\succeq$ 由可加效用函数 $u$ 给出： \[u(x_i)=\begin{cases} 1+(l-i)\epsilon,& 1\leqslant i\leqslant l;\\ (m-i)\epsilon,& l<i\leqslant m. \end{cases}\] 由于“所有由可加效用函数给出的偏好都是responsive的”，故 $\succeq$ 是responsive的. 进一步，当 $\epsilon$ 足够小时，有 $u(S\backslash T)>1/2$，同时 $u(T)<1/2$. 由于 $\succeq$ 是responsive的，且与 $\succeq^{sing}$ 相容，故有 $S\backslash T\succ T$. 因此 $T$ 在 $\succeq^{sing}$ 下不是necessarily agreeable的. 矛盾！故逆命题得证.
综上，原命题得证.

最坏情况的上界

普适的最坏上界

Th 1. 对于 $n$ 个代理人，$m$ 个物品的分配问题，存在 $T\subseteq S$，s.t. \[|T|\leqslant\min\left(\lfloor\frac{m+n}{2}\rfloor,m\right)\] 且 $T$ 对所有代理人都是agreeable的. 进一步，存在特定的偏好，使得该界是紧的.

一般情况的证明较为复杂，先给出了 $n=2$ 的情形：

两个代理人的情形

Proof when $n=2$. 此时上界为 $\lfloor\frac{m+2}{2}\rfloor$. 记两个代理人的偏好分别是 $\succeq_1$ 和 $\succeq_2$.
当 $m=2k+1$ 为奇数时，用反证法：假设不存在至多 $k+1$ 元子集对两个代理人同时保持agreeable.
取 $T\subset S$，s.t. $|T|=k$. 以下先证明一个引理：

引理若 $T\succ_1 S\backslash T$，则 \[(T\cup\{x\})\backslash\{x'\}\succ_1 ((S\backslash T)\backslash \{x\})\cup\{x'\}.\] $\forall x\in S\backslash T$，$x'\in T$.

Proof. 由单调性，有： \[T\cup\{x\}\succ_1(S\backslash T)\backslash\{x\}.\] 此时 $|T\cup\{x\}|=k+1$，由于不存在 $k+1$ 元的agreeable set，故 \[(S\backslash T)\backslash\{x\}\succ_2T\cup\{x\}.\] 进一步，由单调性，有： \[((S\backslash T)\backslash\{x\})\cup\{x'\}\succ_2(T\cup\{x\})\backslash\{x'\}.\] 此时 $|((S\backslash T)\backslash\{x\})\cup\{x'\}|=k+1$，再由不存在 $k+1$ 元的agreeable set，有： \[(T\cup\{x\})\backslash\{x'\}\succ_2((S\backslash T)\backslash\{x\})\cup\{x'\}.\] 至此，引理得证. （只要 $T$ 比其补集更好，则任意与补集交换一件物品后仍然更好.）

继续，不失一般性，设 $\{x_1,\cdots,x_k\}\succ_1\{x_{k+1},\cdots,x_{2k+1}\}$. 反复使用引理，可得： \[\{x_{k+1},x_2,\cdots,x_k\}\succ_1\{x_1,x_{k+2},\cdots,x_{2k+1}\},\] \[\{x_{k+1},x_{k+2},x_3,\cdots,x_k\}\succ_1\{x_1,x_2,x_{k+3},\cdots,x_{2k+1}\},\] \[\cdots\cdots\] \[\{x_{k+1},x_{k+2},\cdots,x_{2k}\}\succ_1\{x_1,x_2,\cdots,x_k,x_{2k+1}\}.\] 由单调性，$\{x_{k+1},x_{k+2},\cdots,x_{2k+1}\}\succ_1\{x_1,x_2,\cdots,x_k\}$，与假设矛盾！奇数情形得证.
当 $m=2k$ 为偶数时，令 $S1=S\backslash\{x_1\}$. 由奇数情形下的结果，存在 $T\subset S'$，s.t. $|T|\leqslant k$ 且 $T\succeq_{1,2} S'\backslash T$. 于是由单调性即可知，$T\cup \{x_1\}$ 即为所求的 $k+1$ 元集合.
综上，命题得证.

上述证明实际上给出了一个多项式时间的算法，可以得到一个至多 $\lfloor\frac{m+2}{2}\rfloor$ 元的agreeable set. 具体过程参见证明，不多赘述.

一般情形的证明

一般情形的证明需要用到所谓Kneser猜想：

Lemma 1. (Kneser 猜想) Kneser图 $KG_{n,k}$ 的染色数为： \[\chi(G)=\begin{cases} n-2k+2, & n\geqslant 2k;\\ 1, & \text{otherwise.} \end{cases}\]

Kneser图的定义如下：

Def X. Kneser图：考虑 $[n]=\{1,\cdots,n\}$ 的 $k$ 元子集族 $\begin{bmatrix} [n] \\ k \end{bmatrix}$，以 $\begin{bmatrix} [n] \\ k \end{bmatrix}$ 为顶点，建立一个 $\binom{n}{k}$ 阶图，结点 $T_1$，$T_2$ 之间有边相连，当且仅当 $T_1\cap T_2=\varnothing$. 这样的图称为Kneser图.

$KG_{5,2}$ 即是大名鼎鼎的Petersen图.
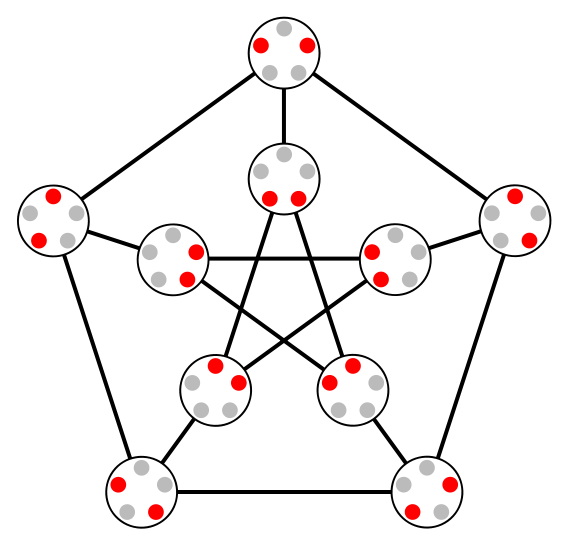
更多Kneser图的形状如下图所示（来源：Wolfram mathworld）

有了这个猜想，即可证明Th 1.

Proof of Th 1. 令 $k=\lfloor\frac{m+n}{2}\rfloor$. 显然 $k\geqslant m$ 的情况是平凡的，只须取 $S$ 为agreeable set即可，故以下只讨论 $k<m$ 的情形.

考虑 $\{x_1,\cdots,x_m\}$ 的 $m-k$ 元子集生成的Kneser图 $KG_{m,m-k}$. 若存在 $T\subset S$，s.t. $|T|=m-k$，且 $S\backslash T\succeq_i T$，$\forall i$，则 $S\backslash T$ 即为所求的 $k$ 元agreeable set.
假设不存在上述这样的 $T$，即 $\forall T\in\begin{bmatrix}S \\ m-k\end{bmatrix}$，都存在 $i$，s.t. $T\succ_i S\backslash T$. 对图 $KG_{m,m-k}$ 染色，给结点 $T$ 染上颜色 $i$，其中 $T\succ_i S\backslash T$. 若有多个 $i$ 对应，任选其一即可.
由于 $k\geqslant m/2$，故 $m\geqslant 2(m-k)$. 由Kneser猜想（Lemma 1.），$KG_{m,m-k}$ 的染色数为： \[\begin{align}\chi(KG_{m,m-k}) &= m-2(m-k)+2 \\ &= 2k-m-2 \\ &\geqslant 2(\frac{m+n-1}{2})-m+2=n+1.\end{align}\] 而上述染色过程只使用了 $n$ 种颜色，故由染色数的定义，至少存在一条边，其两端点共色. 不妨设这两个端点为 $T_1$ 和 $T_2$. 即有，对于某个 $i\in[n]$，$T_1\succ_i S\backslash T_1$，$T_2\succ_i S\backslash T_2$. 但由 $T_1$ 和 $T_2$ 之间有边相连，有 $T_1\cap T_2=\varnothing$，故 $T_1\subset S\backslash T_2$，$T_2\subset S\backslash T_1$. 由单调性立得矛盾： \[S\backslash T_1\succeq_i T_2\succ_i S\backslash T_2\succeq_i T_1\succ_i S\backslash T_1.\] 因此必定存在上述的 $T$，即命题得证.

一组偏好，使得该界是紧的 分为两种情况，以下效用函数均是可加的：

$n\geqslant m$，此时 $\min(k,m)=m$. 取 $u_i(x_j)=\begin{cases} 1, & j=\min(i,m) \\ 0, & j\neq\min(i,m) \end{cases}$，则对代理人 $i$ agreeable的集合必定得包含 $x_{\min(i,m)}$，此时agreeable set必须包含所有物品，共计 $m$ 个；

$n<m$，此时 $\min(k,m)=k$. 对 $i=1,\cdots,n-1$，取 $u_i(x_j)=\begin{cases} 1, & j=i \\ 0, & j\neq i \end{cases}$；同时 $u_n(x_j)=\begin{cases} 1, & j\geqslant n \\ 0, & j< n \end{cases}$. 此时，一个集合若对所有代理人都是agreeable的，则必须包含 $x_1,\cdots,x_{n-1}$，以及 $\{x_n,\cdots,x_m\}$ 的至少一半，共计 $n-1+\lceil\frac{m-n+1}{2}\rceil=\lceil\frac{m+n-1}{2}\rceil=\lfloor\frac{m+n}{2}\rfloor$.

至此，我们已经完成了一般情形的证明，接下来文章对如何获得这样的agreeable set进行了讨论.

获取最坏上界的agreeable set

二人情形

二人情形中，我们只需知道单物品偏好即可得到对二人都necessarily agreeable的集合. 在此我们假设所有偏好是responsive的，并且可以将单物品偏好扩展为 $\mathcal{S}$ 上的偏序.

算法的思路是：按 $1$ 的偏好排序，然后分组，按照 $2$ 的偏好进行选择.

具体的内容由下面的定理给出：

Th 2. （两人情形）给定两个代理人在 $S$ 上的单物品偏好 $\succeq_1^{sing}$ 和 $\succeq_2^{sing}$，存在 $T\subset S$，s.t. $|T|\leqslant \lfloor\frac{m+2}{2}\rfloor$，且 $T$ 对 $\succeq_1^{sing}$ 和 $\succeq_2^{sing}$ 都是necessarily agreeable的. 并且可在多项式时间内求得一个这样的 $T$.
进一步，存在一组偏好，使得这个界是紧的.

Proof. 分奇偶性来讨论：

当 $m=2k+1$ 时，不妨设 $x_1\succeq_1^{sing} x_2\succeq_1^{sing}\cdots\succeq_1^{sing}x_{2k+1}$. 此时按照如下方法进行选择：

$x_1$ 加入集合 $T$；

在 $(x_2,x_3),(x_4,x_5),\cdots,(x_{2k},x_{2k+1})$ 中，每一对都选取 $2$ 更喜欢的那个，加入集合 $T$.

这样选择得到的集合 $T$ 显然对 $\forall j=1,\cdots,m$ 都满足 $|T\cap I_j|\geqslant j/2$，因此由 Prop 1 可知 $T$ 对 $1$ 是necessarily agreeable的. 进一步，由于算法的第2步在每一对中都选择了 $2$ 更喜欢的物品，所以同样可由 Prop 1 知，$T$ 对 $2$ 是necessarily agreeable的.

当 $m=2k$ 时，令 $S'=S\backslash\{x_1\}$. 则由奇数的结果可知，$S'$ 中可以取出一个子集 $T$，s.t. $|T|=k$，且 $T$ 对两位代理人都是necessarily agreeable的. 此时只需将 $x_1$ 也添加进集合，即有 $|T\cup\{x_1\}|=k+1=\lfloor\frac{m+2}{2}\rfloor$，且对二者都是necessarily agreeable的.

综上，命题得证.

一组偏好，使得界是紧的 先不写了，有空再补.

三人情形

三人情形下，无法只使用单物品偏好得到最坏上界的necessarily agreeable set. 以下是一个例子：

Ex. 1. 令 $m=6$，三个人的单物品偏好如下：

$x_1\succ_1^{sing} x_4\succ_1^{sing} x_5\succ_1^{sing} x_6\succ_1^{sing} x_2\succ_1^{sing} x_3$;

$x_2\succ_2^{sing} x_5\succ_2^{sing} x_6\succ_2^{sing} x_4\succ_2^{sing} x_3\succ_2^{sing} x_1$;

$x_3\succ_3^{sing} x_6\succ_3^{sing} x_4\succ_3^{sing} x_5\succ_3^{sing} x_1\succ_3^{sing} x_2$.

若 $T\subset S$ 对三人都是necessarily agreeable的，则必须包含 $\{x_1,x_2,x_3\}$ 以及 $\{x_4,x_5,x_6\}$ 中的至少两个，这样有 $|T|\geqslant 5$. 但是，若知道完整的偏好，由 Th 1 可知，$|T|\leqslant 4$ 即可.

于是三人的情形不能再只使用单物品偏好，需要访问其完整偏好. 考虑到单单是读取完整偏好就已不能在多项式时间内完成，故认为存在一个偏好数据库，我们的多项式时间算法实际上是对该数据库进行多项式次数的访问，每次获取两个集合对于某个代理人的好坏关系.

Th 3. （三人情形）假设存在三个代理人，在 $\mathcal{S}$ 上的偏好分别为 $\succeq_1$，$\succeq_2$，$\succeq_3$. 则存在多项式算法，在多项式时间内可以求得一个 $T\subset S$，s.t. $|T|\leqslant \lfloor\frac{m+3}{2}\rfloor$，且 $T$ 对三个人都是agreeable的.

Proof 仍然分奇偶性来讨论：

当 $m=2k$ 为偶数：我们的目标是找到一个大小为 $\lfloor\frac{m+3}{2}\rfloor=k+1$ 的集合 $T$，使其对三个代理人都是agreeable的. 不妨设 $x_{2k-1}$ 是 $1$ 最喜欢的，$x_{2k}$ 是 $2$ （除 $x_{2k-1}$ 外）最喜欢的，且对于剩下的 $2k-2$ 个元素，有 $x_1\succeq_1\cdots\succeq_1 x_{2k-2}$. （按 $1$ 排序）
记 $A=\{x_1,\cdots,x_{2k-2}\}$，考虑 $(x_1,x_2),(x_3,x_4),\cdots,(x_{2k-3},x_{2k-2})$. 令 $B$ 为上述二元组中 $2$ 不喜欢的元素所构成的 $k-1$ 元集合，则由responsive可知，$A\backslash B\succeq_2 B$.
现考虑一个过程：

只要 $A\backslash B\succeq_2 B$，就取 $B$ 中的一个元素以及 $A\backslash B$ 中与其曾在同一个二元组中的元素，二者交换，形成新的 $B$ 和 $A\backslash B$.

在这个操作中，我们至多进行 $k-1$ 步，就一定能得到一个 $B\succeq_2 A\backslash B$ 的状态. 此时有两种情况，分述如下：

我们根本无需进行任何操作：即 $B\sim_2 A\backslash B$，于是由单调性，可得 $(A\backslash B)\cup\{x_{2k}\}\succeq_2 B$，以及 $B\cup\{x_{2k}\}\succeq_2 A\backslash B$.

我们进行了至少一步的操作：此时，不妨设我们的最后一步操作是将 $x_{2i-1}$ 插入 $B$，并将 $x_{2i}$ 移出 $B$. 令 $C=(A\backslash B\backslash \{x_{2i}\})\cup\{x_{2i-1}\}$，$D=(B\backslash \{x_{2i-1}\})\cup\{x_{2i}\}$，则我们有 $C\succ_2 D$，且 $B\succeq_2 A\backslash B$，并由单调性可得 $C\cup\{x_{2k}\}\succeq_2 D$，且 $B\cup\{x_{2k}\}\succeq_2 A\backslash B$. 至此，我们断言 $D\cup\{x_{2k}\}\succeq_2 C$ 和 $(A\backslash B)\succeq_2 B\cup\{x_{2k}\}$ 中至少有一个成立.

断言的正确性：事实上，若 $C\succ_2 D\cup\{x_{2k}\}$，且 $B\succ_2 (A\backslash B)\cup\{x_{2k}\}$，则 \[C\succ_2 D\cup\{x_{2k}\}\succeq_2 B\succ_2 (A\backslash B)\cup\{x_{2k}\} \succeq_2 C.\] 矛盾！于是断言成立.

至此，两种情况我们都在多项式时间内找到了一个集合 $E\in \begin{bmatrix} A \\ k-1 \end{bmatrix}$，s.t. 包含 $(x_1,x_2),(x_3,x_4),\cdots,(x_{2k-3},x_{2k-2})$ 每个二元组中的恰好一个元素，且满足 \[E\cup \{x_{2k}\}\succeq_2 A\backslash E,~(A\backslash E)\cup\{x_{2k}\}\succeq_2 E.\] （用 $2$ 的偏好调节平衡）
我们即可以如下选取 $k+1$ 元的agreeable set：

选取 $x_{2k-1}$ 和 $x_{2k}$.

按照 $3$ 的喜好选择 $E$ 和 $A\backslash E$ 中较好的那个. （让 $3$ 来选取）

以下证明如此选出的集合 $T$ 对三个代理人都是agreeable的：

$\forall j=1,2,\cdots,m$，$T$ 在 $1$ 最喜欢的前 $j$ 个物品中都至少包含了 $j/2$ 个，故 $T$ 对 $1$ 来说是necessarily agreeable的；

由于 $E\cup\{x_{2k}\}\succeq_2 A\backslash E$，$A\backslash E\cup\{x_{2k}\}\succeq_2 E$，且 $x_{2k-1},x_{2k}\in T$，故 $T$ 对 $2$ 是agreeable的；

由于在 $E$ 和 $A\backslash E$ 中我们选择了 $3$ 偏爱的那个，同时我们选择了剩余的所有元素（$x_{2k-1}$ 和 $x_{2k}$），故 $T$ 对 $3$ 也是agreeable的.

当 $m=2k+1$ 为奇数：此时 $\lfloor\frac{m+3}{2}\rfloor=k+2$，于是只需考虑 $S'=S\backslash\{x_1\}$，利用偶数情形的结果求得满足条件的 $T\subset S'$，此时 $|T|=k+1$. 于是只需取 $T\cup \{x_1\}$ 即可.

综上，命题得证.

求necessarily agreeable的集合

又到了我不喜欢但绕不开的估计和逼近…一大波不等式即将来袭Orz

在此处的讨论中，只需访问每个代理人的单物品偏好即可.

Th 4. 对任意常数个代理人，存在 $T\in\begin{bmatrix}S\\ \frac{m}{2}+O(\log m)\end{bmatrix}$，s.t. $T$ 对所有代理人都是necessarily agreeable的. 这样的集合可在多项式时间内找出.

要证明这个定理，需要一个引理做支持：

Lemma 2. 令 $\sigma_1,\cdots,\sigma_n$ 是集合 $M=\{1,\cdots,m\}$ 的排列. 则存在函数 $f:M\to \{-1,1\}$，.s.t. \[\left| \sum\limits_{i=p}^q f(\sigma_j(i)) \right|\leqslant 8n\log m,~~\forall 1\leqslant p\leqslant q\leqslant m~and~1\leqslant j\leqslant n.\] 进一步，这样的函数可以在多项式时间内被找到.

有了这个引理，即可证明 Th 4.

Proof to Th 4. 设代理人 $j$ 的单物品偏好为 $x_{\sigma_j(1)}\succeq_j^{sing}x_{\sigma_j(2)}\succeq_j^{sing}\cdots\succeq_j^{sing}x_{\sigma_j(m)}$. 由 Lemma 2，我们可以在多项式时间内找到一个函数 $f:S\to\{-1,1\}$，s.t. \[\left| \sum\limits_{i=1}^q f(x_{\sigma_j(i)}) \right|\leqslant 8n\log m,~~\forall q=1,\cdots,m~and~j=1,\cdots,n.\] 现按照如下方法建立一个集合：

将所有满足 $f(x_i)=1$ 的 $x_i$ 加入集合$T$；

剩余物品中，将每个代理人偏好中的前 $\lceil 4n\log m \rceil$ 也加入集合$T$（若某个代理人的偏好中，剩余物品已不足，则全加入集合）.

对 $i=1,\cdots,m$，令 $X_i$ 为指示变量：$X_i=\begin{cases}1, & x_i\in T \\ -1, & x_i\notin T\end{cases}$，则对任意代理人 $j$ 和 $\forall i=1,2,\cdots,m$，有： \[X_{\sigma_j(1)}+X_{\sigma_j(2)}+\cdots+X_{\sigma_j(i)}\geqslant \min\{i, -8n\log m+2\cdot\lceil 4n\log m \rceil\}\geqslant 0.\] 上式意味着：前 $i$ 个物品中在 $T$ 内的个数 $-$ 前 $i$ 个物品中不在 $T$ 内的个数 $\geqslant 0$，即 $\forall i$，$|T\cap I_i|\geqslant i/2$，故由 Prop 1. 可知，$T$ 对 $\forall j$ 都是necessarily agreeable的.

进一步，集合 $T$ 的规模至多为： \[\frac{m}{2}+(n+1)\cdot \lceil 4n\log m \rceil = \frac{m}{2}+O(\log m).\]

综上，命题得证.

进一步，这个界是渐进紧的：

Th 5. 假设 $m=3^k$，$k>0$，则存在三个代理人的单物品偏好，s.t. 所有对三个人都necessarily agreeable的集合都至少具有 $\frac{m}{2}+\Omega(\log m)$ 的规模.

要证明该定理，需要一个引理.

Lemma 3. 给定 $k\in\mathbb{R}^+$，令 $m=3^k$，$M=\{1,2,\cdots,m\}$. 存在三个排列 $\sigma_1,\sigma_2,\sigma_3$，s.t. $\forall f:M\to \{-1,1\}$，记 $\Delta =\sum\nolimits_{i\in M} f(i)\geqslant 1$，则存在 $1\leqslant q\leqslant m$ 和 $1\leqslant j\leqslant 3$，s.t. \[\sum\limits_{i=1}^q f(\sigma_j(i))\leqslant \frac{-k+2\Delta-2}{3}.\]

有了这个引理，即可证明 Th 5：

Proof to Th 5. 设 $\sigma_1,\sigma_2,\sigma_3$ 是 $S=\{x_1,\cdots,x_m\}$ 满足 Lemma 3 的三个排列，对于 $\forall j=1,2,3$，设代理人 $j$ 的偏好是 $x_{\sigma_j(1)}\succeq_j^{sing}x_{\sigma_j(2)}\succeq_j^{sing}\cdots\succeq_j^{sing}x_{\sigma_j(m)}$.
考虑 $\forall T\subset$，s.t. $|T|\leqslant m/2+k/4$. 以下证明 $T$ 不可能同时对三个都是necessarily agreeable的：

构造指示器函数 $f_T:S\to\{-1,1\}$，$f_T(x_i)=\begin{cases}1, & x_i\in T \\ -1, & x_i\notin T\end{cases}$，由于 $|T|\leqslant m/2+k/4$，故 $\Delta_T=\sum\limits_{i=1}^m f(x_i)=|T|-|S\backslash T|\leqslant k/2$.

若 $\Delta_T<0$，则 $T$ 显然不是necessarily agreeable的；

若 $\Delta_T\geqslant 0$，由 $T$ 是奇数且 $\Delta\in\mathbb{Z}$，可知 $\Delta_T\geqslant 1$. 此时由 Lemma 3 可知，$\exists 1\leqslant q\leqslant m$ 和 $1\leqslant j\leqslant 3$，s.t. \[\sum\limits_{i=1}^q f_T(\sigma_j(x_i))\leqslant \frac{-k+2\Delta-2}{3}\leqslant \frac{-k+k-2}{3}<0.\] 即此时 $T$ 也不是necessarily agreeable的.

综上，$T$ 不是necessarily agreeable的. 又由于 $k=\log_3 m$，故necessarily agreeable的集合至少具有 $m/2+\Omega(\log m)$ 的规模. 命题得证.

计算necessarily agreeable set的随机算法

该算法的分析和证明将用到概率论中著名的 Chernoff bound 和 Levy’s inequality：

Lemma 4. (Chernoff bound) 令 $X_1,X_2,\cdots,X_r$ 是 i.i.d. 的随机变量，都服从 ${\rm Pr}[X_i=1]={\rm Pr}[X_i=-1]=1/2$ 的两点分布，记 $X=X_1+\cdots+X_r$，则有： \[{\rm Pr}[|X|\geqslant a]\leqslant \exp(-\frac{a^2}{2r}),~~\forall a\geqslant 0.\]

Lemma 5. (Levy 不等式) 令 $X_1,X_2,\cdots,X_r$ 是 i.i.d. 的随机变量，都服从 ${\rm Pr}[X_i=1]={\rm Pr}[X_i=-1]=1/2$ 的两点分布，记 $Y_i=X_1+\cdots+X_i$，$\forall i$. 则有： \[{\rm Pr}\left[ \max\limits_{1\leqslant i\leqslant r}|Y_i|\geqslant x \right]\leqslant 2{\rm Pr}[|Yr|\geqslant x],~~\forall x\in\mathbb{R}.\]

具体的算法由下述的 Th 6 给出：

Th 6. 假设代理人的数目是常数，取常数 $\epsilon\in (0,1)$，$c>0$，s.t. $\exp(-\frac{c^2}{2})\leqslant \frac{\epsilon}{2n}$（我认为这只是个技术性的条件，用来调节平衡）. 考虑下述的多项式时间算法：

FOR 每个元素，每个元素都有 $1/2$ 概率加入集合 $T$，$1/2$ 概率不加入. 并且当前元素是否加入与其他元素无关；

对每个代理人，将剩余物品中，他们偏好的前 $\lfloor c\sqrt{m}\rfloor$ 位加入集合 $T$.

上述算法至少能以 $1-\epsilon$ 的概率求出一个规模为 $m/2+O(\sqrt{m})$ 的necessarily agreeable的集合.

一点粗浅的理解：
1. 第一步借用 Lemma 4,5 构造一个集合；
2. 第二步补一些元素，把元素个数凑够，满足 Prop 1 的要求.

Proof. 设 $X_1,\cdots,X_m$ 分别是 $x_1,\cdots,x_m$ 的指示变量，$X_i=\begin{cases}1, & x_i\in T\\ -1, & x_i\notin T\end{cases}$，则 $X_1,\cdots,x_m$ 是 i.i.d. 的变量，且都服从 $(1/2,1/2)$ 的两点分布.
对于 $j=1,\cdots,m$，记代理人 $j$ 的单物品偏好为 $x_{\sigma_j(1)}\succeq^{sing}_jx_{\sigma_j(2)}\succeq^{sing}_j\cdots \succeq^{sing}_jx_{\sigma_j(m)}$. 令 $Y_i^j=X_{\sigma_j(1)}+\cdots+X_{\sigma_j(i)}$，$i\in\{1,2,\cdots,n\}$. 取 $a=c\sqrt{m}$，由 Lemma 4，有： \[{\rm Pr}\left[ |Y_m^j|\geqslant c\sqrt{m} \right]\leqslant \exp(-\frac{c^2}{2}).\] 又由 Lemma 5，$X_{\sigma_j(i)}$ 满足：（给 $|T\cap I_i|-|T^c\cap I_i|$ 估界） \[{\rm Pr}\left[ \max\limits_{1\leqslant i\leqslant m} |Y_i^j|\geqslant c\sqrt{m} \right]\leqslant 2\exp(-\frac{c^2}{2}).\] 由于一共有 $n$ 个代理人，每个代理人都满足以上式子，故 \[{\rm Pr}\left[\exists j,~\max\limits_{1\leqslant i\leqslant m} |Y_i^j| \right]\leqslant 2n\cdot c\sqrt{m}\leqslant \epsilon.\] 于是，至少有 $1-\epsilon$ 的概率 $\forall i,j$，$Y_i^j\in [-\lfloor c\sqrt{m}\rfloor,\lfloor c\sqrt{m}\rfloor]$. 考虑到我们在算法的第二步中将所有代理人偏好的前 $\lfloor c\sqrt{m}\rfloor$ 个物品都加入了集合 $T$ 中，这使得 $Y_i^j\geqslant$，$\forall j$. 结合 Prop 1 可知，$T$ 对于所有代理人都是necessarily agreeable的.

由于我们在第一步至多加入了 $m/2+c\sqrt{m}$ 个物品，第二步每个代理人至多加入了 $c\sqrt{m}$，即集合 $T$ 的规模至多是 \[\frac{m}{2}+(n+1)\cdot c\sqrt{m}=\frac{m}{2}+O(\sqrt{m}).\] 命题得证~

一般情形

一般情形下的近似

前文讨论的全部都是一个对所有情况普适的结果，这里我们开始讨论一般的情形. 即，具体的一组偏好，如何找到规模最小的agreeable set？事实上，这个问题可能是困难的，因此这里只提供了一个近似的解.

要解决这个问题，我们首先要处理的就是偏好的问题. 对于给定的 $S$，其子集数量是指数级别，故我们也需要指数级别的空间来存储偏好. 因而任何多项式的算法都无法读取完整的效用函数. 在这里使用value oracle model，即算法可以在确定了 $T\subset S$ 以及 $i=1,2,\cdots,n$ 的情况下，查询 $u_i(T)$ 的值.

文章给出的结果是一个多项式时间的算法，能够计算出近似比为 $O(m/\log m)$ 的近似最优解. 尽管看起来并不好（前文所述的普适上界只有 $O(m)$，此处只优化了 $\Omega(\log m)$），但文章认为这已是多项式时间内可达到的最好情况.

具体的算法分析由以下定理给出：

Th 7. 存在一个多项式时间的 $O(m/\log m)$ 近似算法，能在value oracle model下求出近似最小的agreeable set.

Proof. 将 $S$ 分为 $\lceil\log m\rceil$ 组（注意是不交并），记为 $S_1,\cdots,S_{\lceil\log m\rceil}$，每个组的大小不超过 $\lceil m/\log m \rceil$. 对于每个 $A\subset \{1,2,\cdots,\lceil\log m\rceil\}$，判断 $\bigcup_{i\in A} S_i$ 是否是agreeable的（与其补集比较即可），最后算法输出上述步骤所得到的规模最小的agreeable set. 由于算法中 $A$ 的选取只有 $ m$ 的指数，即 $m$ 的多项式种可能，于是整个算法复杂度是关于 $m,n$ 的多项式.

以下证明算法的近似比是 $O(m/\log m)$：
记最小的agreeable set为 $S^*$，其规模为 $k$. 构造集合 $T=\bigcup_{x\in S^*} (S_i:x\in S_i)$（把 $S^*$ 中所有元素所属的 $S_i$ 并起来），则 $T$ 是我们在算法中检查过的集合，故算法输出的集合规模一定不大于 $T$. 由单调性，$T$ 显然是agreeable的，结合 $|T|\leqslant k\cdot \lceil\log m\rceil$，可知算法输出的集合的规模不会超过最小集合的 $O(m/\log m)$.

得证！

Th 8. 对于每个常数 $c>0$，$\exists m_0$，s.t. $\forall m>m_0$，不存在：只进行不超过 $m^{c/8}$ 次询问，却能得到规模至多是最优解 $m/(c\log m)$ 倍的agreeable set的算法. 即使只有一个代理人，也不行！

Proof. 构造函数 $g(T)=\begin{cases}1,& |T|\geqslant \frac{m}{2};\\ 0,& otherwise.\end{cases}$，进一步，定义 $f_{T^*}(T)=\begin{cases}1, & |T|\geqslant\frac{m}{2}~or~T^*\subset T， \\ 0, & otherwise.\end{cases}$.
考虑只能进行至多 $m^{c/8}$ 次询问的算法 $\mathcal{A}$（暂时假定 $A$ 是确定性的算法），进行如下讨论：

当 $g$ 作为效用函数：设 $\mathcal{A}$ 在运算中查询的所有集合为 $T_1,T_2,\cdots,T_{\lfloor m^{c/8} \rfloor}$；

当 $f_{T^*}$ 作为效用函数：在 $S$ 中随机取一个含 $\lfloor c\log m/4 \rfloor$ 个元素的子集作为 $T^*$，设 $\mathcal{A}$ 在运算中查询的所有集合为 $T'_1,T'_2,\cdots,T'_{\lfloor m^{c/8} \rfloor}$.

考虑任意的 $j=1,2,\cdots,\lfloor m^{c/8} \rfloor$，若 $T_i=T_i'$ 且 $g(T_i)=f_{T^*}(T_i')$，$\forall i=1,\cdots,j-1$，则 $\mathcal{A}$ 在两种效用函数下的计算路径是一样的，因此有 $T_j=T_j'$（？）进一步，若目前为止，两种情况下算法的计算路径相同且 $T_j=T_j'$，我们对 ${\rm Pr}[g(T_j)\neq f_{T^*}(T_j')]$ 有如下估计：

首先，若 $|T_j|\geqslant m/2$，则 $g(T_j)$ 显然与 $f_{T^*}(T_j')$ 相等；若不然，有： \[{\rm Pr}[g(T_j)\neq f_{T^*}(T_j')]=Pr[T^*\subset T_j].\] 若 $|T_j|<|T^*|$，这个概率显然为 $0$. 若不然，由于 $T_j$ 与 $T^*$ 无关，故有： \[\begin{align} {\rm Pr}[T^*\subset T_j] &= \frac{ \binom{|T_j|}{\lfloor c\log m/4 \rfloor} }{ \binom{m}{\lfloor c\log m/4 \rfloor} } \\ &= \left(\frac{|T_j|}{m}\right)\left(\frac{|T_j|-1}{m-1}\right)\cdots\left(\frac{|T_j|-\lfloor c\log m/4 \rfloor+1}{m-\lfloor c\log m/4 \rfloor+1}\right) \\ &\leqslant \frac{|T_j|}{m}^{\lfloor c\log m/4 \rfloor} \\ &\leqslant 2^{-\lfloor c\log m/4 \rfloor} \\ &\leqslant 2m^{-c/4}. \end{align}\]

由 Boole 不等式（union bound），两个序列不完全相同的概率至多是 $(2m^{-c/4})\cdot m^{c/8}$，当 $m$ 较大时显然小于 $1/2$. 进一步，当序列完全相同时，考虑算法 $\mathcal{A}$ 的输出应当是一个在效用函数 $g$ 下也agreeable的集合（？），而由 $g$ 定义即知这样的集合规模至少为 $m/2$. 因此，$\mathcal{A}$ 在效用函数 $f_{T^*}$ 下所输出的集合的规模的期望也至少是 $m/2\cdot 1/2=m/4$. 然而，在 $f_{T^*}$ 下的最优解规模只有 $\lfloor c\log m/4 \rfloor$. 于是，$\mathcal{A}$ 的近似比要大于 $m/(c\log m)$.
最后，当 $\mathcal{A}$ 是随机算法时，也可以对每依次选择的随机性和所有选择的平均值使用以上的方法，并得到类似的结果.

事实上，即使我们要求效用函数是次模函数或次可加函数，上述结果仍然保持. 证明思路类似.

可加效用函数下的情形

是否存在给定大小的agreeable set是NP问题；
- 当 $n\geqslant 2$ 时：是NP完全的；
- 当 $n=1$ 时：贪心即可…
$n\geqslant 2$ 时的证明思路：规约到问题 BALANCED 2-PARTITION.
- BALANCED 2-PARTITION：给定一个多重集非负整数 $A$，判断是否存在 $B\subset A$，s.t. \[|B|=|A\backslash B|=|A|/2,~且~\sum\limits_{x\in B} x=\sum\limits_{x\in A\backslash B}x=\frac{\sum\limits_{x\in A} x}{2}.\]

Lemma 6. BALANCED 2-PARTITION 是NP完全的.

Proof. 从 2-PARTITION 进行规约. （思路：补 $0$）

2-PARTITION 实例：考虑可重集合 $B$，求 $T\subset B$，s.t. $\sum_{x\in T}x=\sum_{x\in B\backslash T} x$.

BALANCED 2-PARTITION 实例：给 $B$ 补 $|B|$ 个 $0$，构成重集 $A$，求 $A$ 的 BALANCED 2-PARTITION.

$\Rightarrow$：设存在 $B$ 的一个 2-PARTITION 解 $T$，则给 $T$ 补上 $|B|-|T|$ 个 $0$，构成集合 $S\subset A$，显然 $S$ 是 $A$ 的一个 BALANCED 2-PARTITION.

$\Leftarrow$：同样，设存在 $A$ 的一个 BALANCED 2-PARTITION 解 $S$，将 $S$ 中原本不在 $B$ 中的元素扔掉（显然都是 $0$），得到 $T\subset B$，则 $T$ 是 $B$ 的一个 2-PARTITION.

Th 9. 设有两个代理人，其偏好都以可加效用函数给出，则“找到一个大小恰好为 $m/2$ 的agreeable set”的问题是NP的.

Proof 从 BALANCED 2-PARTITION 进行规约.

BALANCED 2-PARTITION 实例：$A=\{a_1,\cdots,a_{|A|}\}$.

寻找agreeable set的实例：$S=\{x_1,\cdots,x_{|A|}\}$，$\forall i$，$u_1(x_i)=a_i$，$u_2(x_i)=M-a_i$，其中 $M=\sum_{a\in A}a$.

$\Rightarrow$：若存在 $B\subset A$，s.t. $\sum_{x\in B}x=\frac{\sum_{x\in A} x}{2}$ 且 $|B|=|A|/2. 取 $T=\{x_i:i\in B\}$，则 $T$ 是一个agreeable set（$u_1(T)=u_1(T^c),~u_2(T)=u_2(T^c)$）且 $|T|=|S|/2$.

$\Leftarrow$：设存在一个规模为 $m/2$ 的agreeable set $T$，令 $B$ 为 $T$ 中元素下标所构成的集合. 由于 $T$ 是agreeable set，故 $\sum_{x\in T}u_i(x)\geqslant \sum_{x\in S\backslash T} u_i(x)$，$i=1,2$. $i=1$时，上式意味着 $\sum_{a\in B}a\geqslant \frac{\sum_{a\in A}a}{2}$. $i=2$ 时，上式意味着 $\sum_{a\in B}a\leqslant \frac{\sum_{a\in A}}{2}$. 又易知 $B$ 元素个数为 $A$ 的一半，故 $B$ 是 $A$ 的一个 BALANCED 2-PARTIION.

Th 10. 对任意常数个代理人，其偏好都以可加效用函数给出，则存在一个伪多项式时间的算法（pseudo-polynomial time algorithm），能够求得规模最小的agreeable set.

Proof 用动态规划来解决：

记代理人 $i$ 对所有物品的效用总和为 $\sigma_i$，用 $\Sigma(m',y_1,\cdots,y_n)$ 表示前 $m'$ 个物品 $\{x_1,\cdots,x_{m'}\}$ 中，要使代理人 $i$ 的效用恰好达到 $\y_i$ 的最小所需物品数，其中 $0\leqslant m'\leqslant m$，$0\leqslant y_i\leqslant \sigma_i$，$\forall i$.

初值： - $\Sigma(m',y_1,\cdots,y_n)=\begin{cases} 0, & m'=y_1=\cdots=y_n=0 \\ \infty, & Otherwise \end{cases}$；

转移： - 若 $\forall i$，$u_i(x_{m'})\leqslant y_i$，且 $1+\Sigma(m'-1,y_1-u_1(x_{m'}),\cdots,y_n-u_n(x_{m'}))<\Sigma(m'-1,y_1,\cdots,y_n)$，则（选了 $x_{m'}$） \[\Sigma(m',y_1,\cdots,y_n)=1+\Sigma(m'-1,y_1-u_1(x_{m'}),\cdots,y_n-u_n(x_{m'}))\] - 否则，（不选 $x_{m'}$）\[\Sigma(m',y_1,\cdots,y_n)=\Sigma(m'-1,y_1,\cdots,y_n).\]

最终，我们查找在 $\sigma(...)$ 中是否存在对 $\forall i$ 都有 $y_i\geqslant \sigma_i/2$ 的项，若存在多个，取值最小者即可. 算法复杂度 $O(m\sigma_1\cdots\sigma_n)$.

Th 11. 若代理人数量不是常数，判断是否存在规模为 $\frac{m+1}{2}$ 的agreeable set 的问题是强NP完全的. （强NP完全指不存在伪多项式时间算法，除非 $P=NP$.）

Proof 从 3SAT 进行规约.

3SAT 实例 $\phi$：$n'$ 个变量 $y_1,\cdots,y_{n'}$，$m'$ 个约束 $C_1,\cdots,C_{m'}$.

判断agreeable set存在性的实例： - $n=m'+n'$ 个代理人，记为 $[n]=\{C_1,\cdots,C_{m'},y_1,\cdots,y_{n'}\}$； - $m=2n'+1$ 个物品： - 只有涉及到的代理人才会喜欢的 $\{y_i,\lnot y_i:1\leqslant i\leqslant n'\}$ （共 $2n'$ 个）； - 人见人爱的 $a$ （$1$ 个）. - 效用函数： - $u_{C_i}(b)=\begin{cases} 1, & b=a~或~b~在~C_i~中出现\\ 0, & otherwise \end{cases}$ - $u_{y_i}(b)=\begin{cases} 1, & b=y_i~或~\lnot y_i~或~a \\ 0, & otherwise \end{cases}$

$\Rightarrow$：设 $\phi$ 是可满足的，存在一个解，其中 $y_i$ 的值为 $b_i$. 考虑集合 $T=\{a,b_1,\cdots,b_{n'}\}$. 则对于 $\forall C_j$，$T$ 包含了 $C_j$ 所喜欢的 $y_i$ 的一半，以及 $a$，因而对 $C_j$ 是agreeable的. 另一方面，对 $y_j$ 来说，全集的效用也只有 $3$，而 $u_{y_j}(T)=2$，因而也是agreeable的. 综上，$T$ 是一个规模为 $\frac{m+1}{2}$ 的agreeable set.

$\Leftarrow$：设 $T$ 是一个 $\frac{m+1}{2}$ 元agreeable set. 则 $a\in T$，若不然，可用 $a$ 替换其中任一元素，集合仍是agreeable的.
由于 $T$ 对 $\forall y_i$ 是agreeable的，故对每个 $i$，$T$ 至少包含 $y_i$ 和 $\lnot y_i$ 中至少一者，又由于 $T$ 只有 $n'+1$ 元，故只能对每个 $i$ 恰好包含一者，记为 $b_i$. 现令 $b_i$ 全为真.
又由于 $T$ 对 $\forall C_j$ 是agreeable的，且 $C_j$ 至少涉及到两个 $y_i$，这两个 $y_i$ 至少有一个被设置为真，因此 $\phi$ 被满足.

至此，求最小的agreeable set已经是一个NP问题，因此一个很自然的想法就是求近似解：

Lemma 7. 对任意常数 $\epsilon>0$，存在一个从任意3-SAT条件 $\phi$ 到一个 SET-COVER问题的多项式时间规约 $(U,\mathcal{C}$，以及一个关于 $|U|$ 的多项式函数 $f(U)$，s.t.

(完全性) 若 $\phi$ 是可满足的，则 $(U,\mathcal{C})$ 的最佳值至多为 $f(U)$；

(稳定性) 若 $\phi$ 是不可满足的，则 $(U,\mathcal{C}$ 的最佳值至少为 $((1-\epsilon)\ln|U|)f(U)$.

Th 12. 对任意常数 $\delta>0$，寻找一个规模不大于最优解 $(1-\delta)\ln n$ 倍的agreeable set 的问题是NP完全的.

Th 13. 在偏好函数是可加函数的情形下，求规模不大于最优解 $O(\log n)$ 倍的agreeable set是存在多项式时间解法的.