来自雁栖湖的最大流问题

发表于 | 分类于

\(n\times n\) 的棋盘，有一些障碍物，在没有障碍物的格子上最多放多少个国际象棋的马，使之两两不攻击？

一个和卜凡约饭的中午，突然接到春哥求助这个题.

卜凡瞟了一眼，想都没想，淡定开口：“爆搜.”

一看数据立刻傻了眼：\(200\times 200\)，爆搜必定 TLE… 场面一度十分尴尬（

饭后看手机，发现春哥补刀：有人说是最大独立集，我没搞懂.

于是立刻想明白了…然而春哥自己没有写过.

吃完晚饭突然感到手痒，于是上手写了一发，测过样例直接自信提交，70分！（太菜了吧）

70分！菜鸡！

前七个点 AC 了，后三个点竟然是 RE？

想来想去没有别的地方可能 RE 了，开大边数，直接100分 AC 了.

终于AC...

所以，容我bb一下这道题…

题面

Description

Given a \(N\times N\) chessboard. There are \(M\) obstacles in the chessboard and the position of \(i\)-th obstacle is \((X_i,Y_i)\). You are asked to find the maximum number of knights which can be placed in the chessboard at the same time, satisfied that,

  1. No two knights can attack each other.
  2. Knights can’t be placed in obstacle.
  3. There can be at most one knight in a grid.

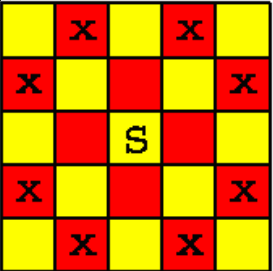
(A Knight in chess can attack 8 positions, as shown in following figure)

国际象棋中的马 走法示意图

Input

Input is given from Standard Imput in the following format:

\(N~M\\ X_1~Y_1\\ X_2~Y_2\\ \cdots\\ X_M~Y_M\)

Output

Print the maximum number of knights.

Sample Input 1

1
2
3
3 2
1 1
3 3

Sample Output 1:

1
5

Test 1: exactly same as sample input 1
Test 2-4: \(1\leqslant N\leqslant 4\)
Test 5-6: \(1\leqslant N\leqslant 6\)
Test 7-10: \(1\leqslant N\leqslant 200\)
For all tests, \(0\leqslant M\leqslant N^2-1\), \(1\leqslant X_i\leqslant N\), \(1\leqslant Y_i\leqslant N\).

思路

一般来说棋盘上“马”的走法用横纵坐标分别来表示：

1
2
const int dx[] = {1, -1, 1, -1, 2, -2, 2, -2};
const int dy[] = {2, -2, -2, 2, 1, -1, -1, 1};

考虑格子的纵坐标之和：马每跳一次，其奇偶性会改变. 用更“组合”的方式说，给棋盘黑白染色后，马每次跳跃的起点和终点格子颜色一定是不同的.

于是考虑按照如下方法建图：

所有没有障碍物的格子视为结点，若马可以从格子 \(a\) 跳到格子 \(b\)，则 \(a,b\) 之间存在一条双向边.

现将所有黑格（\(x+y\) 为偶数）视为一个集合 \(X\)，所有白格（\(x+y\) 为奇数）视为一个集合，则所有的跳跃都发生在 \(X,Y\) 之间，不会发生在 \(X,Y\) 各自的内部，于是这个图是一个二分图.

现在问题所求的是“最多能放多少个马”，即该图最大独立集的大小. 对于二分图，我们有

\[|最大独立集|=总点数-最大匹配数\]

所以只需求其最大匹配. 一般来说有利用匈牙利算法直接求解和利用最大流求解两种方法.

  • 直接用匈牙利算法求解.
  • 最大流方法：（我觉得我不应该说这么详细）
    1. \(X\) 左侧增加一个源点 \(S\)，向 \(X\) 中每一点都连入容量为 \(1\) 的边；
    2. \(Y\) 右侧增加一个汇点 \(T\)，\(Y\) 中每一点都向其连入容量为 \(1\) 的边；
    3. \(X,Y\) 之间的边容量也为 \(1\)（无穷大应该也是有道理的，毕竟源点最多出来 \(1\)）；
    4. 跑一遍最大流（比如dinic），结果即为最大匹配.

代码

第一次因为错误估计了边的数量而 RE 了后三个点，只得70分…后来实在想不到 RE 的点，就开大了很多边数，直接就 AC 了… 细想一下，确实是低估了边数.

提交结果

这里简单说一下正确的边数估计：

棋盘边长是 \(N\)，所以点数大约是 \(N^2\) 级别，考虑到每个点最多 \(8\) 条边，所以总边数绝不超过 \(8N^2\).

带入 \(N\leqslant 200\)，边数至多是 \(8\times 200\times 200=3.2\times 10^5\). 开 maxm = 4e5 就足够了.

最后，因为这是最大流的题目，所以只用了最大流，其实匈牙利算法更短.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
#include <bits/stdc++.h>
using namespace std;

const int maxn = 205; // 注意点数其实是 maxn^2 级别
const int maxm = 1e6; // 所以这里一定要足够大，4e5就够
const int inf = 0x7f7f7f7f;

const int dx[] = {1, -1, 1, -1, 2, -2, 2, -2};
const int dy[] = {-2, 2, 2, -2, 1, -1, -1, 1};

int n, m, tot, Source, Dest;
int dist[maxm], head[maxm];
bool obstacle[maxn][maxn];

struct Edge
{
    int to, nxt, capa;
    Edge() {}
    Edge(int a, int b, int c): to(a), nxt(b), capa(c) {}
} e[maxm];


void addedge(int u, int v, int capa)                     
{
    e[tot] = Edge(v, head[u], capa); head[u] = tot++;
    e[tot] = Edge(u, head[v], 0);    head[v] = tot++;
}

bool bfs() 
{
    memset(dist, -1, sizeof(dist));
    std::queue<int> Q;
    Q.push(Source);
    dist[Source] = 0;
    while (!Q.empty())
    {
        int x = Q.front();
        Q.pop();
        for (int i = head[x]; i != -1; i = e[i].nxt)
        {
            int y = e[i].to;
            if (e[i].capa && dist[y] == -1)
            {
                dist[y] = dist[x] + 1;
                Q.push(y);
                if (y == Dest)
                    return true;
            }
        }
    }
    return false;
}

int dfs(int x, int exp) 
{
    if (x == Dest || !exp)
        return exp;
    int ret(0), tmp;
    for (int i = head[x]; i != -1; i = e[i].nxt)
    {
        int y = e[i].to;
        if (dist[x] + 1 == dist[y] && e[i].capa)
        {
            ret += (tmp = dfs(y, min(exp - ret, e[i].capa)));
            e[i].capa -= tmp;
            e[i ^ 1].capa += tmp;
        }
    }
    if (!ret) dist[x] = -1;
    return ret;
}

int dinic()
{
    int ret(0);
    while (bfs())
        ret += dfs(Source, inf); 
    return ret;             
}

// 以上全部是模板

void init(int s, int t)
{
    Source = s;
    Dest = t;
    memset(head, -1, sizeof(head));
}

bool judge(int x, int y) // 判定(x, y) 格子是否可以放马
{
    if(x < 1 || x > n) return false; // x 不能越界
    if(y < 1 || y > n) return false; // y 不能越界
    return !obstacle[x][y]; // 不能有障碍物
}

int f(int x, int y) // 二维变一维
{
    return (x - 1) * n + y;
}

int main()
{
    cin >> n >> m; // 懒，用了cin cout
    for(int i = 0; i < m; i++)
    {
        int x, y;
        cin >> x >> y; // 还是懒...
        obstacle[x][y] = true;
    }

    init(0, n * n + 1);

    for (int x = 1; x <= n; x++)
    {
        for (int y = 1; y <= n; y++)
        {
            if (obstacle[x][y]) continue; 
            if ((x + y) & 1)
            {
                addedge(Source, f(x, y), 1); 

                for (int _ = 0; _ < 8; _++)
                {
                    int xx = x + dx[_];
                    int yy = y + dy[_];

                    if (judge(xx, yy))
                        addedge(f(x, y), f(xx, yy), 1); // 边权为inf亲测也没问题
                }
            }
            else
            { 
                addedge(f(x, y), Dest, 1);
            }
        }
    }
    printf("%d", n * n - m - dinic()); // 输出不懒了！

    return 0;
}