疫情影响不能出门,在家又玩起了魔方…接触魔方已有很多年,玩过十几种不同的魔方了,把一些东西记录下来,给自己看. (被迫学习了一波
canvas+js画图…)
- 符号说明
- 233 魔方还原方法(网上的相关资源不多,且质量不高)
- 5 阶魔方的棱
- 三阶魔方奇奇怪怪的姿势(×)
描述魔方转动的记号——Singmaster Notation
简单来说,就是用符号来表示魔方的转动.
现行的符号体系图解参见 http://www.mf100.org/base/about.php
比起那种平平无奇(×)的定义,我更想递归描述一下(什么毛病?)
那么我要开始了…(×)
先定义一下字符集:
- 字母——表示旋转
- 单面操作:
U D L R F B,分别表示上下左右前后面(单面)顺时针旋转90°; - 双面操作:
u d l r f b,分别表示上下左右前后面(双面)顺时针旋转90°,i.e. 单面+中间层一起转; - 中层操作:
E M S(不是特快专递):E:U和D的夹层做D方向的旋转;M:L和R的夹层做L方向的旋转;S:F和B的夹层做F方向的旋转;
- 整体操作:
x y z,分别表示魔方整体向着R U F方向旋转90°;
- 单面操作:
- 逆向符号——逆操作,可以视为 \(a^{-1}\).
',可以加在所有字母后面,使得旋转方向变为逆时针.- 例如:
U'表示顶面逆时针旋转90°.
- 括号——编组
- 表示将括号内的字符串编为一组. 不加括号时,单个字母(包括其后的
')自成一组.
- 表示将括号内的字符串编为一组. 不加括号时,单个字母(包括其后的
- 数字——表示重复执行次数(幂次)
- \(\forall n\in N_+\),可以跟在单个字母(包括其后的
')后,或完整的组之后,表示重复执行 \(n\) 次.- 例如:
U2表示顶面旋转180°.
- 例如:
- \(\forall n\in N_+\),可以跟在单个字母(包括其后的
现在,我们可以说,公式就是由下面几条所定义的东西:
- 空语句
e是公式,表示什么都不做; - 若
A是公式,n是数字,则(A)以及(A)n是公式; - 若
A是公式,c是字母,则Ac、cA、Ac'、c'A是公式;
公式应当是可以化简的:
- 设
c是字母,则相邻的cc'以及c'c可以消去; - 若括号中只有单个字母,则该括号可以扔掉(废话;
- 以上步骤可以反复进行,直到没有任何可以消去的东西,那么这个公式应该就是最简的了(吧?)
上述内容既没有经过查证,也没有经过严格的复核…如有疏漏之处还请指正(
233 魔方还原
还原方法:底层十字(很简单)\(\to\)底层角块\(\to\)顶层角块\(\to\)顶层棱块.
233 魔方相比三阶魔方,有一些特殊之处:
- 侧面的棱只能转 180 度,不能转 90 度. (
LRFB都必须连做两次). - 底面还原好后,顶面也一定还原好了.
- 事实上,233 魔方只有位置的变化,总变化数为 \(7!\times 8!\times 2=406425600\).
据说可以视为三阶魔方去掉中间层,进而以三阶魔方的
F2L以及PLL稍作改动来还原… 奈何本人才疏学浅,尝试几次却不得要领.
底层十字很好做,因此从底层角块开始
底层角块
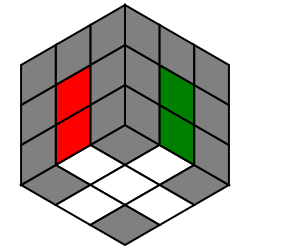
我们只需要解决下图中的情形:
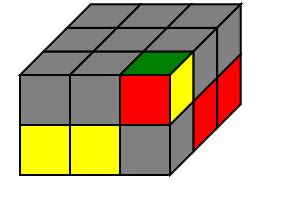
1 | 解决方法:R2U R2U' R2 |
- 注意:该方法能够完整保留底层所有其他块的位置不动,但不能保证顶层的其余块不动.
顶层角块
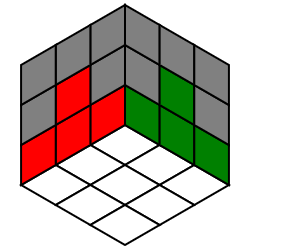
我们只需要实现“交换相邻角块”的操作即可(暂时不管上层棱块). 事实上,我们可以解决下图所示的情形(交换一组相邻角块以及一组相对的棱块):
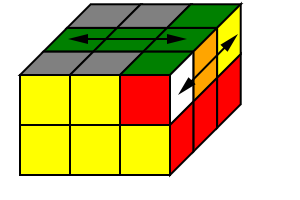
1 | 解决方法:R2U R2U' R2 F2U' F2U F2U' |
- 注意,上述操作的前一半与还原底层角块时的操作完全一样,因此前一半实际上将图中的
红-白-绿块放到了底面.
顶层棱块
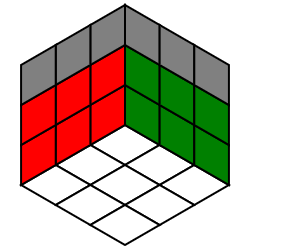
顶层棱块需要两种操作:1. 交换相对的棱块,2. 交换相邻的棱块.
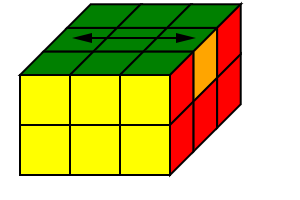
|
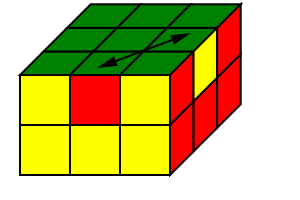
|
| 相对棱块交换示意图 | 相邻棱块交换示意图 |
|---|
对于相对棱块的情形,直接做三次 R2U2 即可.
- 上述操作能够完美保证其他所有块的位置和朝向均不发生变化. 因此可利用该操作还原相邻棱块的情形.
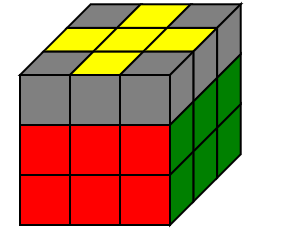
事实上,对于相邻棱块,先做 R2 D B2,即可将右边的棱块(图中第二层右边的黄色棱块)转移到背面,此时就变成了相对的情形,按照相对棱块的办法复原,再还原即可.
1 | 解决方法: |
其他操作
可以做的一些其他操作.
两层同时交换相邻的棱块和角块
解决如下情形:
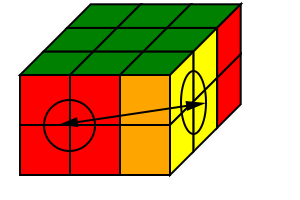
1 | 解决方法:R2U'R2U DR2D'R2 |
同时调整第二层的三个棱块
解决如下两种情形:
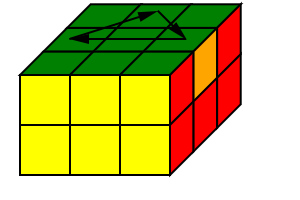
|
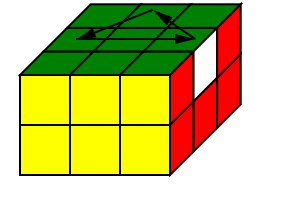
|
| 棱块顺时针轮换示意图 | 棱块逆时针轮换示意图 |
|---|
1 | 解决方法: |
参考资料
- http://affairs.ymhs.tyc.edu.tw/reheart/RC/th/3x3x2.htm
此外,还有一种类似于三阶魔方“缺角层先法”的还原思路,参考 http://www.soongsky.com/cube/solve233/
五阶魔方的棱
翻棱
常规的拼棱方法是把两侧的棱块逐个(按照正确的方向)拼到最中间的棱块上. 事实上,只需要如下的一个公式:
1 | RUR' FR'F'R |
- 该公式的效果是把
R面和F面交叉的棱翻转过来,具体可以在三阶魔方上验证.
最后一组棱
最后一组棱可能会出现位置对但方向不对的情况,如下图所示:
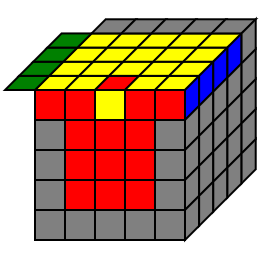
1 | 解决方法:r2 B2 U2 l U2 r' U2 r U2 F2 r F2 l' B2 r2 |
- 上述操作同时也会将图中
蓝-黄和绿-黄位置的两组棱以及角块互换,其他块保持不变.- 不过好像并没有什么实质作用…
- 比较有用的说法是:上述操作不会破坏其他已经拼好的棱
84 拼棱法
三阶魔方的各种玩法
先贴一个关于解法之间的比较:
知乎 为什么很多人都采取层先法?https://www.zhihu.com/question/59164976
层先
相关资源特别多:
- 一个从第一层开始教学的教程:
- 一个简洁但内容足够充分的教程:
但是,层先法有着不同的路数..
我最初接触的层先法
笔者从初中(大约11年或者12年)开始接触魔方. 好像是在太原某超市买了一个10元上下的魔方(品牌好像是永俊?),对着说明书研究了一个中午搞会了还原方法…那本说明书很短但很清晰,算是我的启蒙导师吧…因此,凭借自己(应该比较靠谱)的回忆,在这里描述一下这个还原方法:
| 底面做十字 | 复原底面角块 | 复原中层棱块 | 顶面做十字 | 复原顶面角块 | 复原顶层棱块 |
|---|---|---|---|---|---|
|
|
|
|
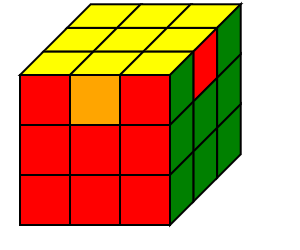
|
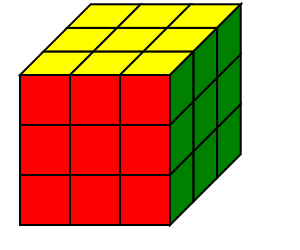
|
具体用到的公式及简略说明:
1 | 第一层就不多bb了... |
很容易发现上述公式有一些可以简化的部分…随意列出几条:
- 做顶面十字时,可能需要连续操作 2 或 3 次
R' U' F U F R,此时相邻的R和R'可以抵消. 调整顶层棱块位置时(以顺时针为例):我们需要做的是
R U R'U R U2 R'U'+ R'U'R U'R'U2 R U. 其中,“+” 前的最后一个U'是在调整顶层的角度,使得可以不转动魔方而直接套用角块朝向公式. 但实际上这一步是多余的,因而在角块的方向还原(R'U'R U'R'U2 R)后,我们需要做额外的一步U来还原顶层角度. 我们可以旋转整个魔方,来简化这个操作. 简化后的公式为:1
2逆时针:L'U'L U'L'U2 L + y + L U L'U L U2 L'
顺时针:R U R'U R U2 R'+ y'+ R'U'R U'R'U2 R仍然是调整顶层棱块位置时,对于以下情况需要做两次公式. 但可以有一个替代的方案,步数大约是原先的一半:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20考虑以下情形——相邻棱块两两互换. 按照公式有如下解法:
O4O O2O O1O 这里是做两次顺时针轮换(243)和(124)
1O3 -> 1O4 -> 4O2 解法不唯一.
O2O O3O O3O
但是我们可以考虑如下操作:
- M S D S' D2 M'
** 该操作的效果为:
1. 交换UF棱块与UR棱块
2. 交换DB棱块与DL棱块(注意,涉及到的四个棱块恰好分列LRFB四个侧面)
3. 底层错位90度(相当于做了一次 D)
因此我们对上述情况:
1. 先做一次 MSDS'D2M',复原顶层的一组相邻棱块.
2. 然后做一次 D',使得未被复原的棱块分列四个侧面.
3. 此时将魔方整个水平旋转180度(y2),再做一次 MSDS'D2M',即可将棱块全部复原.
4. 最后再做 D',将底面角度调整好即可.
综上所述,交换顶面两组相邻棱块时,可以采取下述公式,减少步数:
- MSDS'D2M' D' y2 MSDS'D2M' D'
** 不过其中使用了太多的中间层操作,在速度上未必会有显著提升.
** 事实上,CFOP 的 PLL 中还有更好的做法.
网站 rubiks-cu.be
网站 rubiks-cu.be 同样给出了一种还原方法. 在顶面十字做好后,后续操作与上一套做法有些不同:
| 底面做十字 | 复原底面角块 | 复原中层棱块 | 顶面做十字 | 复原顶层棱块 | 复原顶层角块 |
|---|---|---|---|---|---|

|

|

|

|
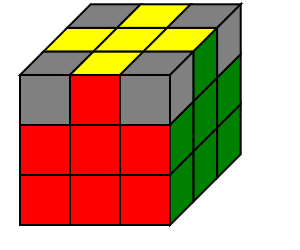
|

|
这里引起我注意的主要是棱块位置的还原,以及角块的轮换:
- 关于顶面棱块的位置,这里给出的公式是
RUR'URU2R'U. 与上一套做法中最后一步“轮换棱块”的公式的前一半基本相同. 该网站对此公式的说明“swap edges”,事实上相当贴切…因为这个操作的效果就是交换UF棱块与UL棱块. - 关于角块的轮换,给出了一种不同的公式:
1
2
3
4
5
6
7先给出公式:U R U' L' U R' U' L
其作用如下:(俯视图,上为F,下为B,左为L,右为R)
2O1 1O3 即:除FRU角块外的其余三个角块逆时针轮换.
OOO -> OOO
3OX 2OX
** 该公式能保持所有棱块不发生任何变化,但会改变顶层角块朝向
** 其对顶层角块带来的朝向改变与上一套中相应公式带来的变化不同
这里对角块朝向的处理也非常有趣:
1 | 只需要反复做 R'D'RD,就必定可以将FRU角块还原.(为什么?值得思考) |
GAN 说明书
参考链接:https://www.gancube.com/layer-by-layer-guide-of-gancube
2020年寒假期间在家突然想起了魔方,但是先前的魔方已经找不到了(大概是送给别人了),因此买了一个 GAN 的魔方,其说明书比较长,包括了层先法与 CFOP. 这里给出的层先法也是非常有 “CFOP 味道” 的一种做法:
| 底面十字 | 底面角块 | 中层棱块 | 顶面棱块朝向 | 顶面角块朝向 | 顶面角块位置 | 顶面棱块位置 |
|---|---|---|---|---|---|---|

|

|

|

|
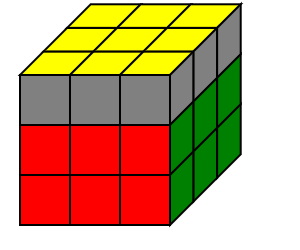
|
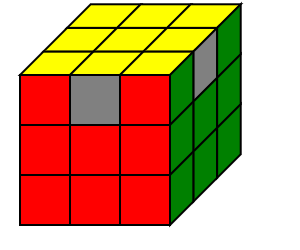
|

|
前四步与先前的所有层先法都完全相同. 在还原顶面角块朝向时,使用的公式与第一套做法中的公式相同. 值得关注的主要是角块位置的还原:
1 | 这一步只用到一个公式:(R'U) (L'U2) (RU') (R'U2) LR |
GAN教程中的最后一步使用的是 M'2 U M U2 M' U M'2,不过并没有什么值得关注的地方.
升级版层先法——CFOP
又名 Fridrich 方法,分为 Cross, F2L, OLL, PLL 四步,所以一般叫 CFOP:
C-底层十字:Cross,无公式F-前两层:F2L(First 2 Layers),41 个公式O-顶面块朝向:OLL(Orientation of Last Layer),57 个公式P-顶面块位置:PLL(Permutation of Last Layer),21 个公式
| 底层做十字 | 还原前两层 | 还原顶面朝向 | 还原顶面位置 |
|---|---|---|---|

|

|

|

|
总公式量为 \(41+57+21=119\).
CFOP 详见: http://www.rubik.com.cn/fridrichold.htm
另有一篇介绍了 8 种速解方法的文章:
角先
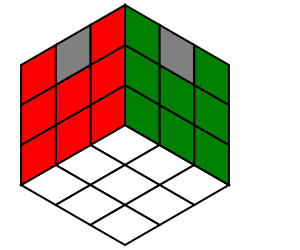
还原步骤:
| 底层角块 | 顶层角块 | 中层棱块 | 底层棱块 | 顶层棱块 |
|---|---|---|---|---|
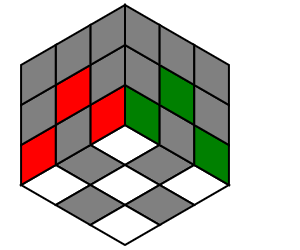
|
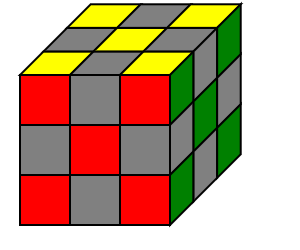
|
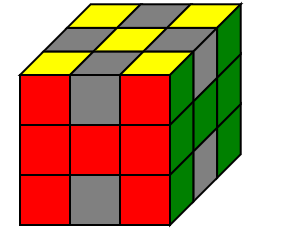
|
|

|
还原所有角块
1
2底层角块:很容易,无公式
顶层角块:可以使用层先法调整顶层角块的公式还原中层棱块
1
只有一个公式:M' R U' M U R'
- 还原底层棱块:很容易,琢磨一下即可(
还原顶层棱块朝向(EOLL):
1
2
3
4
5
6
7
8
9翻转一组相邻棱块(FU和RU):
- M U M' U2 M U M'
** 实际上只需要这一个公式好像就够了...
翻转一组相对棱块(FU和BU):
- (x') M' U' R U M U' R' U (x)
四个棱块同时翻转:
- M' U2 M U2 M' U M U2 M' U2 M还原顶层棱块位置(EPLL):同层先法.
参考 https://www.speedsolving.com/wiki/index.php/Corners_First
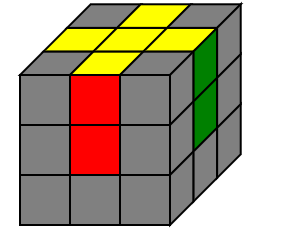
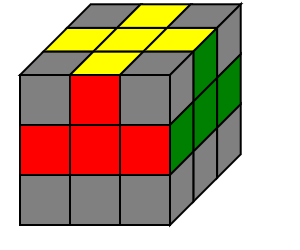
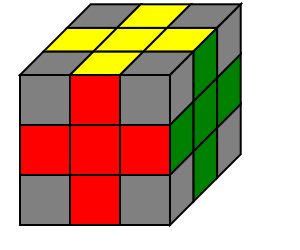
棱先
棱先法已经基本被抛弃了…
| 顶层十字 | 中层棱块 | 底层棱块 | 复原角块 |
|---|---|---|---|
|
|
|

|
- 1990s Rubiks.com solution:https://web.archive.org/web/20020208140757/http://www.rubiks.com:80/cubesolution_new.html
- 古老的解法……属于棱先法
- 棱先法还有多种变化,参考 https://www.speedsolving.com/wiki/index.php/Edges_First
- 一个中文的资料:http://roburchou.lofter.com/post/1d235558_686872c
桥式(Roux method)
常用于最小步还原的一种还原方法,参见 https://www.speedsolving.com/wiki/index.php/Roux_method
其他方法
- 缺角层先法:http://www.soongsky.com/cube/solve/
- Columns First Methods:https://www.speedsolving.com/wiki/index.php/Columns_First_Methods
魔方资源整理
直接搜的话太过零散了…做个简单整理(
- 速解相关:https://www.speedsolving.com/wiki/index.php/Main_Page
- 五魔方相关:http://www.mf100.org/megaminx/wumo.php
- 二阶五魔方只需要顶层的角块公式,其余自己摸索就很容易做出.
- sq-1 魔方相关:http://www.mf100.org/sq1/index.htm
- 最小步数还原:http://fmcsolves.cubing.net/fmc_tutorial_ENG.odt