许老师《现代图论》课中所讲授的四色猜想的相关内容.
基础知识
一些相关概念介绍如下（图的定义、Euler公式、Kuratowski定理等不再赘述）：
图的染色（着色） 给图的顶点赋权（一般为整数，当然，不是整数也可以强行调整为整数…），相邻顶点不同权.
四色猜想 任意平面图都是可以 \(4\)-染色的.
导出子图 设有图 \(G=(V,E)\)，及其顶点集的子集 \(V'\subset V\)，记 \(E'=\{(u,v)\in E:u,v\in W\}\)，则称 \(G'(V')=(V',E')\) 为 \(V'\) 的导出子图.
- 随便举个例子吧：\(K_n\) 的任意 \(m\) 元子集的导出子图都是 \(K_m\). （当然，\(m\leqslant n\) …）
极大平面图 顾名思义，就是边已经多到极限的平面图，以至于再加一条边，它就不是平面图了.
- 极大平面图又称三角剖分图，其每个面都是三角（二维单形就是三角，课上许老师没有提单形的故事，但其实单形剖分是在任何维度存在的）；
- 任何一个图都可以通过不断加边而变成一个极大平面图。
符号说明
- \(n\)：点数；
- \(m\)：边数；
- \(\delta\)：图中顶点的最小度数.
关键术语：
- Kempe 链：只含两种颜色的链.
- Kempe 变换：一种通过换色来减少颜色的技巧.
Kempe 的证明思路
用数学归纳法：
- 容易验证 \(n\leqslant 5\) 时，所有的极大平面图都可以被 \(4\)-染色.
- 设 \(n\leqslant p\) 时，所有 \(n\) 个顶点的极大平面图都可以被 \(4\)-染色，考虑 \(p+1\) 的情. 由 Euler 公式可知，对于极大平面图，有 \(3\leqslant \delta\leqslant 5\)，故分三种情况讨论：
- \(\delta=3\)：
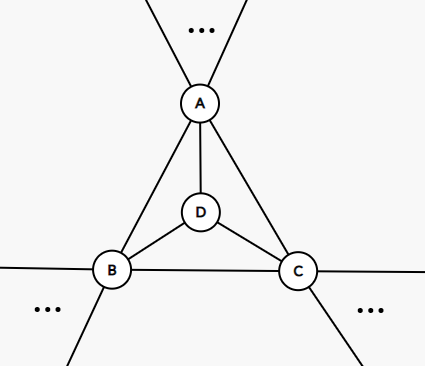由于 \(\delta=3\)，故必定会存在一个 \(3\) 度顶点，即有图中所示的结构. 记 \(G'=G-D\)，则 \(|G'|=p\)，因而可以被 \(4\)-染色. 而 \(D\) 相邻的 \(A,B,C\) 点也至多占掉三种颜色，故此时的图 \(G\) 是可以被 \(4\)-染色的. - \(\delta=4\)：
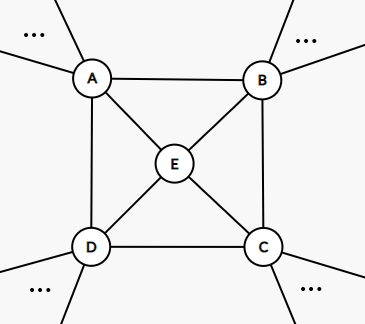同上，会存在一个图示的结构，记 \(G'=G-E\)，则 \(G'\) 有一个 \(4\)-染色. 若 \(A,B,C,D\) 只用了至多 \(3\) 种颜色，则可以完全沿用上述方法. 因此只讨论 \(A,B,C,D\) 分别用了颜色 \(1,2,3,4\) 的情形. 此时采用的办法被称为 Kempe 变换：
考虑 \(G'\) 中，颜色 \(1\) 和 \(3\) 的导出子图 \(G'[1,3]\)：- 若 \(A\) 和 \(C\) 不在 \(G'[1,3]\) 的同一个连通分支内，则可以将其中一者（不妨设是 \(A\)）所在的连通分支上的 \(1\) 与 \(3\) 全部交换，该种转换不会产生颜色的冲突. 转换完毕后，\(A\) 与 \(C\) 将变为同色，即 \(A,B,C,D\) 只占三种颜色；
- 若 \(A\) 和 \(C\) 在 \(G'[1,3]\) 的同一连通分支内，则必定存在一条连接 \(A\) 与 \(C\) 的 \(1-3-1-3-\cdots\) 路径（这样的路径称为 Kempe 链）. 此时考虑 \(G'[2,4]\)，则 \(B\) 和 \(D\) 一定不在 \(G'[2,4]\) 的同一连通分支内（有点像 Jordan 闭曲线定理的那种感觉，\(B\) 和 \(D\) 一个在内一个在外），即可以对 \(G'[2,4]\) 做变换，此时也可转换为 \(A,B,C,D\) 只占三种颜色的情形.
- \(\delta=5\)：
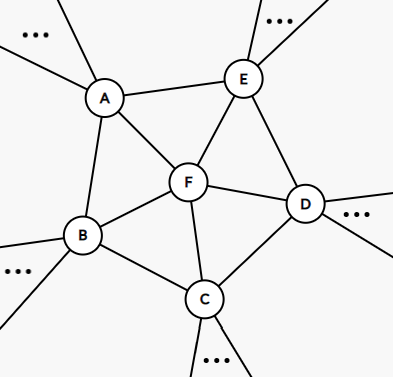同样会存在一个图示的结构，记 \(G'=G-F\)，则 \(G'\) 存在一个 \(4\)-染色. 若 \(A,B,C,D,E\) 只用了至多 \(3\) 种颜色，则很容易给出该种情形的一个 \(4\)-染色. 当 \(A,B,C,D,E\) 恰好用了 \(4\) 种颜色时，必定有且仅有两个顶点同色，不失一般性，设 \(f(A)=1,f(B)=f(E)=2,f(C)=3,f(D)=4\). 此时考虑 \(G'[1,3]\) 和 \(G'[1,4]\)：
- 若 \(A,C\) 和 \(A,D\) 至少有一对在相应的导出子图上不连通，则可以直接采取换色的方式消灭掉颜色 \(1\)，此时在 \(G\) 中给 \(F\) 染颜色 \(1\) 即可.
- 若 \(A,C\) 和 \(A,D\) 在相应的导出子图上都连通，则在 \(G'\) 中存在一条连接 \(A,C\) 的 \(1-3-1-3\cdots\) 链和一条连接 \(A,D\) 的 \(2-4-2-4\cdots\) 链，分别将 \(B\) 与 \(E\) 包围. 故类似 \(\delta=4\) 的情况，不难发现此时不存在 \(E\to C\) 和 \(B\to C\) 的 Kempe 链，因而进行两次换色，即可将颜色 \(2\) 消除. 进一步给 \(F\) 染颜色 \(4\) 即可得到 \(G\) 的 \(4\)-染色.
- \(\delta=3\)：
听起来很简单，不是吗？但很遗憾这个证法是错误的. 错误的关键就在于：虽然图中有一条 \(A\to C\) 和一条 \(A\to D\) 的 Kempe 链，但这两条链可能在处 \(A\) 点之外的其他地方也有交点，这可能会导致我们在后面消除颜色 \(2\) 的换色过程中失败.
听起来好绕啊！那就详细说说…
当 \(\delta=5\)，且 \(|f\{A,B,C,D,E\}|=4\)，且 \(A,C\) 在 \(G'[1,3]\) 中连通，\(A,D\) 在 \(G'[1,4]\) 中连通时，我们需要进行两次换色：
- 在 \(G'[2,3]\) 中，将 \(E\) 所在的连通分支中的所有 \(2\) 和 \(3\) 对换，即可将 \(E\) 换为颜色 \(3\).
- 在 \(G'[2,4]\) 中，将 \(B\) 所在的连通分支中的所有 \(2\) 和 \(4\) 对换，即可将 \(B\) 换为颜色 \(4\).
两次换色后，\(A,B,C,D,E\) 的颜色分别为 \(1,4,3,4,3\)，成功减少了一种颜色！
那么，问题出在哪里呢？
就是上述过程中，第一次换色完全可能影响到第二次换色.
试想，如果第一次换色使得 \(B\) 和 \(D\) 在 \(G'[2,4]\) 中连通了怎么办？第二次换色就无法进行了！！那我们构造 \(G\) 的 \(4\)-染色的计划就失败了（
那么，什么情况会导致第二次换色失败呢？
我们要让第一次和第二次换色产生关系. 因此我们努力让它们换色的前提产生关系. 那就是说，我们要让 \(A\to C\) 的 Kempe 链与 \(A\to D\) 的 Kempe 链在 \(A\) 以外的一点相交，这样两次换色就可以互相干扰了.
事实上，Heawood 给出的反例正是应用了这个思路. 其具体的反例如下图所示：
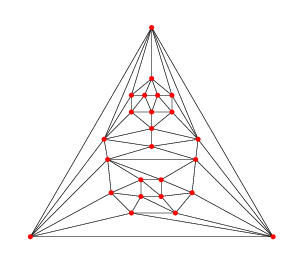
虽然 Kempe 没有成功证明四色定理，但 Kempe 的工作仍然是非常有意义的，在其做法的基础上稍加改动，即可证明比四色定理稍弱的五色定理. 后来 Appel–Haken 对 Kempe 变换失效的不可约情形进行了研究，并利用计算机给出了证明.
对 Kempe 工作的进一步思考
既然两条 Kempe 链相交会导致 Kempe 变换失效，那么我们就需要寻找不相交的 Kempe 链.
Mr. Xu 的猜想！ 对于 \(\delta=5\) 的情形，对任意一个 \(5\) 度顶点 \(v_0\)（\(N(v_0)=\{v_1,v_2,v_3,v_4,v_5\}\)），都存在 \(G'\) 的一种染色方案 \(f\)，s.t. 存在 \(v_1\to v_3\) 和 \(v_1\to v_4\) 两条 Kempe 链，且这两条链仅在 \(v_1\) 相交.
若能证明这个猜想，那当然能修复 Kempe 的证明.（不过我8太看好…
- 貌似 Heawood 的图中，中心的 \(5\) 度顶点就根本不行…
- 我始终觉得这个猜想只需要存在性就行了（存在一个 \(5\) 度顶点…），但 Mr. Xu 课上说的的确是任意… 迷惑…