数学系转专业考试题及解答不完全版（2015.04）

北京师范大学数学科学学院转专业考试. 2015年4月.

几句废话

又是一年转专业的时候, 转专业这件事也又一次被提起。最初的转专业想法是在刚入校形成的, 经历了一些波折之后最终确定了转专业的事情, 于是在2015年的4月（其实也可能是3月, 记不清了）参加了转专业的考试。笔试结果出来之后得知洲洲没有通过笔试, 洲洲希望我能整理一份题目和解答给他（或许是留作纪念）。但由于考完之后没有很及时地整理, 导致了个别问题的遗漏（至多两个）。整理完之后将纸质版交给了洲洲, 为了保存一下相关内容, 我便将该文档拍照发到了我的贴吧：lzcwr吧里边。但是由于我当时过于naive, 还不懂得“图像压缩”的问题, 便直接将画质很差的图像上传到了网上。。导致帖子里边的图片全部是AV画质。。有兴趣可以点击原帖地址看看。。现在想起来有点后悔, 于是决定重新整理一份（在较大程度上能还原原试卷）。

试题

设数列 $ { x_n } $ 满足 $x_n>0$, 且 $\forall n\in \mathbb{N}$, 都有 $x_{n+1}+\frac{1}{x_n}<2$, 求证：\[\lim_{n\to\infty}x_n=1\]
若函数 $f(x)$ 满足 \[f(x+y)=f(x)\times f(y)\]且 $f(0)=1$, $f'(0)=2$, 求 $f(x)$ 的表达式.
求极限：\[\lim\limits_{x\to0}\frac{\sin x^6}{x^2-\arcsin x^2}\]
设 $f(x)=x^3\sin2x$, 求：$f^{(10)}(0)$.
求积分：\[\int_0^{\frac{\pi}{4}}\frac{x\sec^2x{\rm d}x}{(1+\tan x)^2}\]
求证：\[\frac{2}{3}n\sqrt{n}<1+\sqrt{2}+\sqrt{3}+\cdots+\sqrt{n}<\frac{4n+3}{6}\sqrt{n}\]
令 $f(x)=xe^{-x}$, 设 $f(x)$ 有极值点 $(x_1,y_1)$, 拐点 $(x_2,y_2)$：
1. 求 $(x_1,y_1)$ 和 $(x_2,y_2)$.
2. 求函数与 $x$ 轴在 $x=x_1$ 与 $x=x_2$ 之间围成的面积.
令 $f(x)$ 为定义在 $(-\infty,+\infty)$ 上的函数, 且对 $\forall x\in\mathbb{R}$, 均有 $|f(x)|\leq M_1$, $|f''(x)|\leq M_2$, 求证：\[|f'(x)|\leq \sqrt{2M_1M_2}\]

解答

因为我比较懒。。一些简单题目就不做详细的解答了。。一定要看详细解答的可以去原帖看av画质的图片, 应该能看懂。。（别问我为什么不用有序列表）

1.由条件, $x_{n+1}-x_n<2-(x_n+\frac{1}{x_n})$, 而由均值不等式有 $x_n+\frac{1}{x_n}\geq 2$, 于是 $x_{n+1}-x_n<0$, 即数列 $ { x_n } $递减。于是数列 $ { x_n } $单调有界, 有极限。由 $x_{n+1}+\frac{1}{x_n}<2$ 易得结论；

2.两边同时取对数即变为 Cauchy 方程 $g(x+y)=g(x)+g(y)$, 用 Cauchy 方法即可求解；

3.换元 $y=x^2$ 后将分子分母分别泰勒展开至 $y^3$ 即可得答案为 $-6$；

4.这个题不会做自觉面壁；

5.无脑积分：md劳资怎么改都generate不了, 只好截个图算了。。

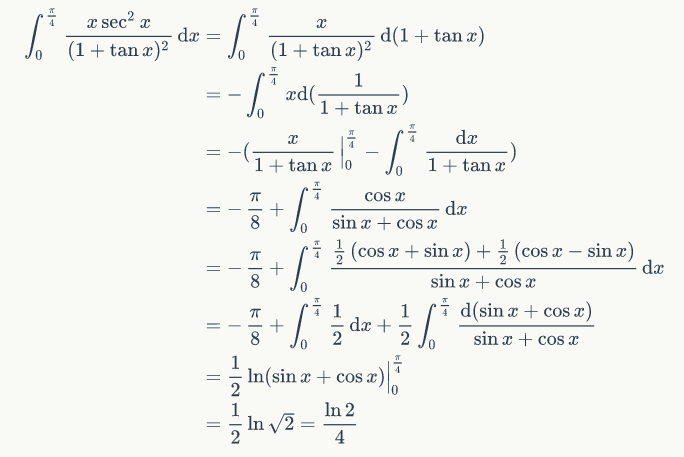
6.一方面考虑 $f(x)=\sqrt{x}$ 在 $[0,n]$ 的积分, 有 $\sum_{i=1}^{n}\sqrt{i}>\int_0^n\sqrt{x}{\rm d}x=\frac{2}{3}n\sqrt{n}$；另一边不等式只需给右边做差, 证明 $\sqrt{k}<\frac{4k+3}{6}\sqrt{k}-\frac{4k-1}{6}\sqrt{k-1}$ 即可（不会做的自觉面壁）；

7.这个题不会做的继续面壁吧；

8.考场上没做出来, 后来问会了但是现在也不记得了……比较难, 这样的题考场上做不出来可以理解。

祝要转专业的各位转专业成功！

不能忍。。存一下第五题的公式代码……问题解决了再贴上去……

\begin{align}
\int_0^{\frac{\pi}{4}}\frac{x\sec^2x}{(1+\tan x)^2}{\rm d}x &= \int_0^{\frac{\pi}{4}}\frac{x}{(1+\tan x)^2}{\rm d}(1+\tan x) \\
 &= -\int_0^{\frac{\pi}{4}}x{\rm d}(\frac{1}{1+\tan x}) \\
 &= -(\frac{x}{1+\tan x}\Big|_0^{\frac{\pi}{4}}-\int_0^{\frac{\pi}{4}}\frac{{\rm d}x}{1+\tan x}) \\
 &= -\frac{\pi}{8}+\int_0^{\frac{\pi}{4}}\frac{\cos x}{\sin x+\cos x}{\rm d}x \\
 &= -\frac{\pi}{8}+\int_0^{\frac{\pi}{4}}\frac{\frac{1}{2}(\cos x+\sin x)+\frac{1}{2}(\cos x-\sin x)}{\sin x+\cos x}{\rm d}x \\
 &= -\frac{\pi}{8}+\int_0^{\frac{\pi}{4}}\frac{1}{2}{\rm d}x+\frac{1}{2}\int_0^{\frac{\pi}{4}}\frac{{\rm d}(\sin x+\cos x)}{\sin x+\cos x} \\
 &= \frac{1}{2}\ln(\sin x+\cos x)\vert_0^{\frac{\pi}{4}} \\
 &= \frac{1}{2}\ln\sqrt{2} = \frac{\ln2}{4}
\end{align}